
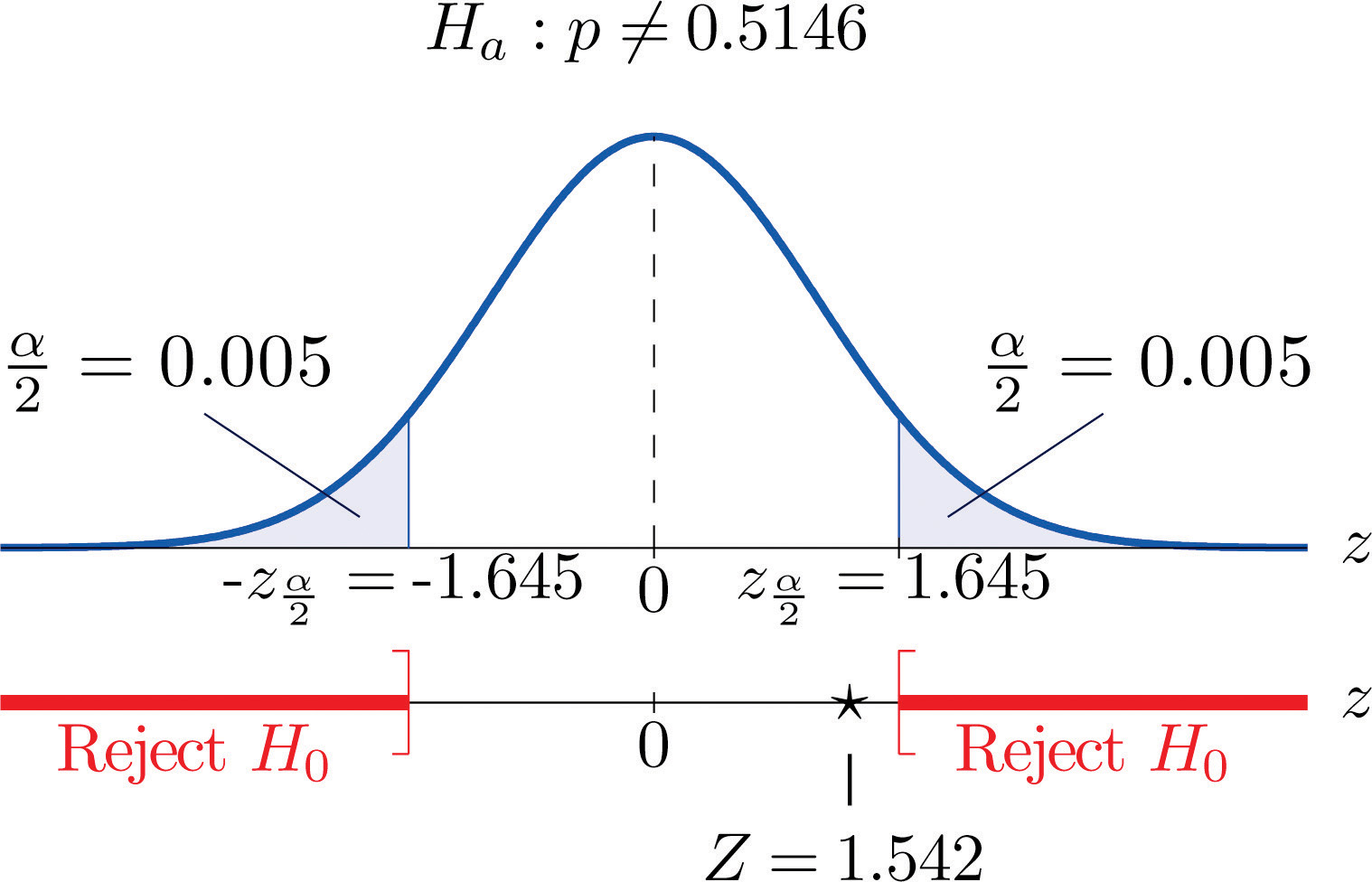
Left tail hypothesis testing is illustrated below: There is left tail, right tail, and two tail hypothesis testing. There are 3 types of hypothesis testing that we can do. The smaller the significance level, the greater the nonrejection area. So the greater the significance level, the smaller or narrower the nonrejection area. This means that there is a greater chance a hypothesis will be rejected and a narrowerĬhance you have of accepting the hypothesis, since the nonrejection area decreases. You increase the significance level, the greater area of rejection there is. If you choose a significance level of 20%, you increase the rejection area of the standard normal curve to 20% of the 100%. If you choose a significance level of 5%, you are increasing Of 1%, you are choosing a normal standard distribution that has a rejection area of 1% of the total 100%. Therefore, if you choose to calculate with a significance level The total rejection area of a normal standard curve. The significance level that you select will determine how broad of an area the rejection area will be. So when we do our testing, we see which hypothesis is actually true, the null (claimed) or the alternative (what we believe it is). The alternative hypothesis is that μ > 20, which In this case, the null hypothesis is the claimed hypothesis by the company, that the average complaints is 20 (μ=20). The alternative hypothesis is the hypothesis that we believe it actually is.įor example, let's say that a company claims it only receives 20 consumer complaints on average a year.
The null hypothesis is the hypothesis that is claimed and that we will test against. We accept true hypotheses and reject false hypotheses. Whether we accept or reject the hypothesis.
So, this script omits the numbers on top of the bars.This Hypothesis Testing Calculator determines whether an alternative hypothesis is true or not. Since the bars are very thin, if we put numbers on top of them, the result will be a mess. Here is the R script used to create the above barplot. Which indicates the sample provides statistically significant evidence that the claim is true because theįigure for Question 6. $\rho > 60\%$ĭata: If in a sample of 10 students 8 of them like math, the sample supports the claim because $\dfrac = P(X \geq 115 \ \mid \rho = 51\%)$ Claim: more than 60% of students like math.If the data from the sample agrees with (or supports) the claim, we say the data provides evidence that the claim is true. We test a claim by taking a sample from the population.



 0 kommentar(er)
0 kommentar(er)
